Finally, we come to statistics. To follow how these link together, you may want to first read previous posts about Percentages and Probability. Probability is about determining a value to define the likelihood of an event or a hypothesis. Statistics is a branch of math that involves collecting, sorting, analyzing and interpreting data. Statistics makes use of probability in evaluating the applicable data. A summary of both can be found here. Since probability has other uses but is integral to statistics, we might see the interface as something like this:
 In the post about probability, I mentioned that we would not discuss all details about how probability is measured and the calculations needed to analyze more complex conditional probabilities. Statistics likely has more opportunity for rabbit holes to chase. I will not chase all of those but will highlight key points to demonstrate how statistics must be used carefully. Since this post will address more misuse or numbers and methods, it will be a longer read. If you have some understanding of statistics and uses of data, you may want to jump to “Misuse of Statistics”.
In the post about probability, I mentioned that we would not discuss all details about how probability is measured and the calculations needed to analyze more complex conditional probabilities. Statistics likely has more opportunity for rabbit holes to chase. I will not chase all of those but will highlight key points to demonstrate how statistics must be used carefully. Since this post will address more misuse or numbers and methods, it will be a longer read. If you have some understanding of statistics and uses of data, you may want to jump to “Misuse of Statistics”.
Origins
As with probability, we are interested in statistics as a mathematical concept and, perhaps, a science. Statistics and probability developed separately but advanced in parallel. As with other areas of math, the theory and application of both have grown over time. Statistics probably began as early population studies. How many women with children lived in a certain village? What was the average height of adult males age 20 in a certain state? As the knowledge of the methods grew, their use was expanded into other areas for which data was to be analyzed. This now includes both analysis of data (what does the data tell use about a sample and a population?) and use of data to make predictions about populations.
Long Introduction
In probability, we look at sample spaces, events, conditions, and likelihood.
A statistic, is a set of data from part of a “population“. The population includes every member of the group in which we have interest. If we want statistics on 16 ounce carpenter’s hammers, the population would be all available brands and makes of those hammers. Each would have slightly different characteristics – head shape, claw shape, handle length, handle material, etc. These are some of the category variables in our statistic. (The study of statistics involves many other types of variables that we won’t cover in this post.)
Since it’s unlikely that we can locate “all” such hammers, we can only consider a part of the population. Let’s assume we select the ten models of these hammers that are available at the local hardware store. Those ten hammers together are a “sample” from the population. With those ten hammers, we can develop a set of data. From that data, we would have a statistic. We could then provide an estimate of the data for all such hammers in the entire population. Since we only have ten hammers, we would be making very large assumptions about the population from our data on those hammers. Instead, let’s consider another type of statistics and compare the ten hammers to each other.
If you do an internet search for “best hammers” or “best” anything, you will get different lists. Some will overlap. The author of the “best of” article may have either a certain bias or, like us, will only evaluate a limited portion of the population. Similarly, let’s say we want to determine the “best” hammer. We will choose certain data to evaluate. Maybe we choose the following (I recognize that some of these may be impractical):
- Durability of the striking face – measured by changes in the face (does it deform?) of the hammer head after we drive 500, 16d framing nails into a 2X4.
- Comfort of the handle – this might be smoothness, size, slipperiness when wet, and general shape. These are subjective.
- Balance – how well are the head and handle weight balanced while still delivering a sound blow to the nail? We could possibly measure balance.
- Overall weight – is the hammer excessively (subjective) light or heavy? We can weigh each hammer.
- Nail pulling – how well does the shape and design of the claws support ease of pulling nails? Unless we have a machine that measures pull strength requirements, this is probably subjective.
Here are the results of our testing. We chose to grade each hammer in each category from 0 to 100. (Assume we developed a procedure for testing and some criteria for scoring.)
| BRAND >> | Acme 106 | HH 2745 | Hitter AVU | Hard Hitter | Easy Pull | Comfort Grip | Aces All | Every Day | 1942 | Jo’s Best | Average |
| Durability | 35 | 50 | 70 | 65 | 60 | 55 | 40 | 80 | 65 | 75 | 59.5 |
| Comfort | 40 | 55 | 65 | 70 | 70 | 75 | 60 | 55 | 60 | 65 | 61.5 |
| Balance | 50 | 60 | 60 | 75 | 55 | 60 | 50 | 60 | 55 | 65 | 59 |
| Weight | 80 | 55 | 60 | 75 | 65 | 70 | 55 | 70 | 70 | 70 | 67 |
| Pulling | 30 | 50 | 70 | 80 | 80 | 75 | 50 | 60 | 70 | 75 | 64 |
| Average | 47 | 54 | 65 | 73 | 66 | 67 | 51 | 65 | 64 | 70 | 62.2 |
From this evaluation, we now have a set of data that we can compare to determine which hammer ranks “best”.
Limitations
In our selection of best hammer, we chosen ten hammers from possibly hundreds in the population, but we’ve also only evaluated each hammer based on five criteria. Some things to consider as we made our ranking or if we plan to use this data for estimates about all hammers:
- Our data set is small. For estimating the population, this raises question about whether or not this could be a “representative sample” of the population.
- Our criteria for testing may or may not be the most vital for hammer tests. Would a carpenter who uses a hammer every day for work find these to be the important measures?
- Our selection is local. Could the local selection also be regional favorites that aren’t common throughout the population?
If we’re only interested in fame from defining “the best 16 ounce carpenter hammer”, we may not care about what’s missing from our evaluation. Most people who see our decision won’t care about those either. But for more serious endeavors such as determining the effectiveness of a new drug for a common health issue, the collection of data, the size of the population, and the items we choose to evaluate to determine the drug’s effectiveness have more weight. Much more weight than 16 ounces.
This is often the nature of evaluating data for determining a population statistic. We haven’t sampled the whole, we have chosen criteria we believe are worth measuring, and we have used some undefined techniques to evaluate our criteria. We also can’t tell, from the information presented, how we came up with those scores. How is a score of 70 in hardness different from a score of 35? For a statistical evaluation that has more merit, we need to understand how these were tested, how they were scored, was the testing/scoring method suitable to provide consistent scores, etc.
If we did want to use our test data to estimate characteristics of the population of hammers, how could we translate it to the population with any confidence? Let’s look at some more details about statistics.
Interpreting Statistics
Admittedly, in our example of data and in data from scientific studies, we must recognize that this sample may or may not represent the population. If we want to believe our results and be able to sell our conclusions to others, we need to think about our goals and methods.
- Before we begin collecting data, we need to define our goal. What do we expect to learn from the data? Why is that important? What benefit could this offer?
- As with our discussion about defining probability conditions, we need to clearly define the conditions surrounding our testing and data collection. The conditions we define have an impact on interpreting the results. Similarly, when someone else sees our conclusions, they know the limitations.
- We need a way to account for both errors in our samples (they don’t represent the population) and in our tests. Sampling and testing may not be exact.
- We need a method to estimate the population based on data from our sample.
Data
In our hammer sample, we collected the data from our own test design and our own testing. Data for use in statistics may come from testing where we know the background or data may come from sources of information generated by someone else. The hammer testing we imagined above is a very simple set of numbers. More likely, businesses, scientists, or others will use sets of data that have a very large set of information. Instead of using 50 data points as with our hammer test, data sets often have thousands or millions of data points. A key part of statistics is understanding that the data is consistent and complete enough for a valid evaluation. There is much being written now about how to select and evaluate data. We will not discuss that here.
Evaluation Types
Statistical methods can have one of several goals in evaluating a data set. Some of these are included below. We will not explore these in depth, but they help us understand the many ways that data can be analyzed. These are simplified definitions of some common types:
- Descriptive – our task may simply be to collect, sort, and analyze data to present the characteristics of the information. This is often in graphical form to show what the data set contains.
- Inferential – in this case, we are analyzing a data set to reach some conclusion. What can we infer from the data?
- Predictive – this method looks at the past trends in data and makes conclusions about possible future trends.
- Prescriptive – here we analyze the data with the goal to make recommendations about future actions.
- Exploratory – we may first want to look at a data set to determine patterns, missing information, or other characteristics of the available data.
- Causal – data may be able to help us determine a cause and effect relationship from information contained in the data set.
Statistical Measures
There are many measures that can be made on a data set. What and how we measure will vary with our intended evaluation. Here are a few measurements that are often used in statistical evaluation:
- Mean – we used the Mean in our table of hammer data. The mean is the average. Our table shows an average for each brand and an average for each of the characteristics we measured.
- Standard Deviation – this is a common method for looking at data. It tells us how much the data varies about the mean. In the hammer data, we can see that Durability has a mean value of 59.5 but ranges from 35 (24.5 below the mean) to 80 (20.5 above the mean). What does this variation around the mean tell use about the hammers and the data?
- Hypothesis Testing – many studies begin with an assumption or theory (hypothesis). Data is collected to help determine whether or not the hypothesis is true, false, or undetermined. In the hammer tests, we could have started out assuming that all hammers in the test would show very good results in nail pulling and durability testing. Our data showed that these results varied considerably. If were testing that hypothesis, we might say that is failed – our group of hammers was not consistently good at nail pulling and some did not do well in a main purpose of hammers (driving nails).
Interpretation
The goal in evaluating data using statistical methods is to reach a conclusion, gain insight into the current state of some situation, determine needs for action, or simply to have a better understanding of our data. If we have sound testing, clean data (i.e., there are no gaps in data and we believe the values are valid), and unbiased evaluation, we can learn what we need to know. As the goal becomes more predictive, data is less reliable, and we must add in assumptions, our analysis may or may not be valid.
Misuse of Statistics
We won’t review the calculations related to statistics. Those details are beyond the scope of this post. But, we can see that, with the possible complexity of selecting, cleaning, sorting, analyzing, and interpreting a data set, we can make unintentional errors. Our data set may be skewed, invalid, or may contain gaps. Though modern data analysis has developed methods for filling in gaps, those methods require decisions. Our analysis may be based, unknowingly, on invalid assumptions about our data. Errors in this series of steps may lead to invalid conclusions. This type of error is not what I’ll discuss below as the misuse of statistics. “Misuse” here implies a deliberate altering or misrepresentation of results.
Though scientific and mathematical studies should yield objective answers (except where there may be many unknowns or when a new theory is being tested), they can be altered or misused to show a certain result. We can find this misuse or alteration more frequently in issues related to political results and business objectives. If I hold a position in government and want my new bill to be favored, I may want this so much that a “scientific study” using statistics becomes altered to show more beneficial results. If I am a regional manager presenting my business plan, I may want my predictive statistics supporting my plan to skew toward a positive outlook. If I am reporting business results, how could I present those results so that they look (at least) more favorable.
Here are three ways that use of data can skew actual results. Some of these may involve issues related to percentages or probabilities.
Presentation
Data is often presented in graphical form because a “picture” of results is often more readable than a massive data table. One variable involved with preparing a graph is the determination of the scale. If we graphed the hammer test results for Hardness where the x-axis is the brand score and the y-axis shows the individual test result, we can select the scale of the y-axis.
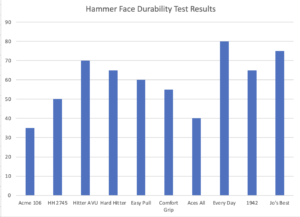
In this example, Excel selected the y-axis scale allowing this graph to visually show the differences in Durability test results. We can easily see how some results are lower and some are higher. However, if we change the y-axis scale, the variation in results is not as obvious.
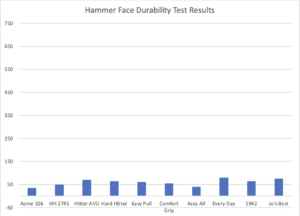
The bars showing Durability still vary in height but because the y-axis scale is (ridiculously) altered, they don’t appear to vary as much. One could interpret this new graph to mean that the Durability results were similar for all hammers. Though this graph makes it obvious that the y-axis skews the visual results, this graph could be presented without showing the y-axis scale values.
There are other ways to show results in a way that alters the true picture. This can be from using a graph type that does not show a clear picture of by other misuses of scale.
Data Summaries
This series of posts started with a discussion of percentages. Some of that was very basic information. Sometimes it’s in the interpretation of percentages that results can be “managed”. Sometimes this involves use of “relative” vs “absolute” percentages.
Assume a test result says that 2% of people are likely to develop a certain disease within their lifetime. Scientists suspect that this can be influenced by age, diet, and genetics. A diet high in vegetables (to throw a curve into the normal discussion) is expected to increase the risk of the disease. Studies showed that 3% of people with a high vegetable diet are likely to develop the disease. The absolute difference in this likelihood is 1% (i.e., 3% – 2% = 1%). But, using relative percentages to show differences presents a different picture.
The relative risk is 50%. The relative risk compares the absolute risk with the average 2% risk (i.e., 3% – 2% = 1%; 1% / 2% => 50%). If you have the disease, you don’t care about these results. But, if you eat a high-vegetable diet and wonder if you should reduce your intake of fresh vegetables, how do you decide? You need to understand the source of numbers when making such decisions.
These small numbers (2% and 3%) seem insignificant and they may be. But when the differences in test results can be portrayed as either 1% or 50%, it matters. It may be shocking to learn that these studies showed a 50% increase in likelihood of catching a disease if you have a high-vegetable diet. It is less dramatic when you see the difference as only 1%. Though the numbers we used showed that the differences were minor in absolute terms, this study could also have been presented as “High Levels of Vegetables in the Diet Leads to 50% Increased Risk of Disease”.
In the hammer testing, we could have reason to influence interpretation of the results.The Durability for the Every Day brand was 80. The Durability for Jo’s Best was 75. Acme 106 has a score of 35. Every Day may see this study and want to present it in the best light. How can they report that their brand is better in this category?
- They could claim their Durability scores were 5 points greater than the nearest competitor. That doesn’t seem to be a significant difference.
- They could claim their hammer was 7% (i.e., 5 / 75 = 0.067) better than the nearest competitor. Still not significant.
- They could go with a more generic claim (which we likely see more often than we realize) that their hammer tested “as much as 129% better than competitor models” (80 – 35 [Acme 106] = 45; 45 / 35 => 129%).
- They could use even more deceptive numbers. The Every Day hammer scored 20 point below 100 (20%). The Jo’s Best hammer scored 25 points below 100 (25%). That difference is 5 or 5%. If I compare the 5% to the Every Day 20%, I could claim the Every Day Durability results were 25% (i.e., 5 / 20 = 0.25 = 25%) better than those of Jo’s Best. (Yes – that is a convoluted way to compare but this demonstrates that you can rationalize many types of comparisons to present a positive result.)
Improper Correlation and Causation
Correlation involves linking two sets of results (or two variables) together to show a relationship between them. Correlation can be positive or negative. If Variable A shows an increase (or decrease) as Variable B increases (or decreases), these are positively correlated. If one consistently decreases as the other increases, this is a sign of a negative correlation. Perhaps you own a stock that increases whenever the S&P 500 increases. Your stock price decreases whenever the S&P 500 decreases. Your stock’s price is positively correlated with the S&P 500 Index.
Results of testing can either incorrectly or deliberately make improper comparisons. A famous example is from the New England Journal of Medicine (registration or subscription may be required – read more here) which suggested that the level of consumption of chocolate in a country was correlated with the country’s number of Nobel prize winners. So, if you eat a lot of chocolate, you may be more likely to win a Nobel prize. This is a misuse, perhaps in this case as an error and not as a deliberate misuse, of correlation. Discussion of correlation brings up a related issue with correlation – the common phrase: “Correlation does not imply causation”. Though this article was later reported to have been a tongue-in-cheek report (here and here), it is a good illustration.
Causation occurs when something “causes” something else. If your stock price increases/decreases with the S&P 500, they are positively correlated but it does not mean that your stock’s price change caused a change in the S&P 500. If two things show positive correlation, it may not be true that this means one thing caused the other. We must be careful about the conclusions we draw from our data.
However, we can use correlation and causation to deliberately misrepresent data. The theory that chocolate consumption leads to increased intelligence and thus produces more Nobel prize winners would be a good report for a chocolate company to use to attempt to increase sales.
So What?
This has been a lengthy discussion about topics related to statistics and use of data. Hopefully some of it was educational if you aren’t familiar with these topics. After 3,000+ words, what are the takeaways?
- Statistics is considerably more complicated as a method to evaluate data. We have not really touched on the complexity of estimating the validity of results, the error in our data, or how data can be translated to a conclusion.
- If steps aren’t taken with care, results can be wrong. Even with modern software packages and algorithms built into Excel for calculating statistical results, “garbage in => garbage out” is still true.
- Don’t skew our data to fit a hypothesis. Don’t skew data or its presentation to show a false positive result. Once we’ve made it past the hurdle of calculating accurate statistical results, we can still be guilty of presenting results in a way that presents them more positively than the actual results.
Next, I will post a shorter summary article that brings these three together.
